Introduction

Severe earthquakes that have occurred in recent years have caused severe financial losses to governments and people. Therefore, seismic engineering researchers realized the need to correctly estimate earthquake hazards' risk and provide logical solutions to reduce it. Risk is usually identified by three components: risk (earthquake), capital (structure), and the relationship between capital and risk. Due to the random nature of earthquakes and the uncertain parameters of the structure, the relationship between the behavior of the structure and the earthquake is always determined by uncertainty and uncertainty. Actual structures are often irregular, and the common assumption of structure is idealistic. In a general category, different types of height irregularities can be divided into two categories: geometric and non-geometric irregularities. In geometric irregularities in height, the dimensions of the structural plan change significantly, such as buildings with recoil or retreat in height, and buildings with geometric shapes are prominent types of this irregularity. In non-geometric irregularities in height, sudden changes in the dynamic properties of the structure, including mass, stiffness, and lateral strength, occur along the height. The cause of this type of irregularity includes the difference in the use of different floors of the structure, the presence of an extra heavy mass on one floor, the difference in the height of the floors, the removal of braces or shear walls in the parking floor of the structure and so on.

Introduction

Iran is always at the top of the countries where earthquakes have been associated with many human and financial losses [1-3]. On the other hand, the growing need of urban society for space in large cities and the lack of necessary space leads to the development of some existing buildings. These extensions, which must be made according to the applicable capacity for the building, can lead to irregularities imposed on the building, and these imposed irregularities affect the seismic behavior of the building. An earthquake is a natural phenomenon that occasionally shakes a part of the earth and causes damage. Since Iran is one of the seismic regions of the world, the need to deal with this natural phenomenon is strongly felt [4]. In recent years, many financial and human losses have been caused to the country by earthquakes. One of the main issues in the seismic design of buildings is the proper configuration of their plan to prevent the increase of imposed torsional anchors due to structural irregularities. The presence of irregularities in the structures, especially during an earthquake, causes torsion in the structure, which leads to an intensification of displacements and seismic forces entering the structure. The presence of irregularities in the structure in its seismic behavior imposes certain complexities that make the analysis difficult. For example, the effects of higher modes, especially torsional modes, on the seismic behavior of the structure are sometimes greater than the initial modes, or the deformation of the structure is completely transformed, or different parts of the structure have unique periods. For this reason, irregular structures need special ductility and strength, and to analyze them, methods are needed to consider these requirements and complexities. In any case, it should be noted that the amount and type of disorder are very effective in causing the type and amount of damage. The existence of elevation irregularities due to the non-uniform distribution of physical geometric properties in the height of the building can lead to an unwanted concentration of nonlinear deformations during an earthquake and lead to local or general destruction. Vulnerability is a term used to indicate potential damage to communities, buildings, and geographical areas due to natural disasters. Assessing the seismic vulnerability of existing buildings is, in fact, a kind of prediction of their damage against possible earthquakes. Every year, several earthquakes of different magnitudes occur in the country, especially in areas with high seismicity, which cause severe damage and casualties. In strong and destructive earthquakes, the effect of an earthquake on irregular buildings is far greater than the effects obtained by assuming linear behavior and using equivalent static analysis according to the recommendations of building codes. Assessing the needs imposed by an earthquake in such a situation requires nonlinear dynamic analysis. It differs from the initial assumption of regularity that uses equivalent static analysis in its design, and certainly, the actual behavior of the building is different from what is considered. One of the most important steps in analyzing the seismic performance of structures is to evaluate and analyze their behavior in the non-elastic response range. A comprehensive breakdown analysis can provide structural status at various stages of lateral loading, from linear elastic behavior to the moment of complete collapse. However, the evaluation of the collapse capacity of structures and attention to the descending branch of the behavior and capacity of the structure after its maximum response through the analysis of increasing nonlinear dynamic time history using nonlinear behavioral models in a series of different and decremental strengths. This sue has been the focus of much attention over the past decade. Structural irregularities are unavoidable in many urban structures due to architectural, functional, and economic constraints [5]. In seismic areas, determining the seismic behavior of structures and recognizing their behavior against earthquake waves is very important. The performance of regular and irregular buildings against earthquakes is different, so irregular buildings are more vulnerable than regular buildings and more likely to collapse than traditional buildings. Inaccurate approximations in structural analysis models that ignore the effects of the connection source can lead to inadequate estimation of the seismic needs of the structure. Using a weak connection spring reduces the need for structural components but increases the deformation of the structure. On the other hand, a strong connection spring causes the beam's flexural strength to reduce the structure's deformation, but the need for structural components increases. Due to the importance of the effect of the connection spring and its interaction with the type of earthquake, this study investigates the nonlinear dynamic behavior of steel flexural frames by considering the connection spring in the area around the fault. Therefore, due to the importance of this issue in this research, the nonlinear performance of irregularly high-grade steel structures in height and the possibility of their failure will be investigated. Another point is that research has not paid attention to the role of the connection spring and its positive and negative effects. In contrast, it will have a significant effect on the behavior of the structure.

Ahmadi and his colleagues in 2017, in a study entitled Seismic evaluation of tall steel buildings with bracing core system and arm restraint using fragility curves and damage profiles. The type of arms restraint and truss belt structures is very effective in reducing the response of tall structures to lateral loads. However, the existing design regulations do not mention arm restraint as a seismic system. In this study, the seismic behavior of tall buildings with arm restraint is investigated, and the effect of adding arm restraint on the seismic capacity corresponding to the collapse level performance level, demand corresponding to the onset of general instability, how seismic demand is distributed at height and fragility curves at the threshold performance level Collapse is studied. For this purpose, three buildings of 20, 25, and 30 floors are designed in three dimensions so that the effects of arms restraint are not considered in the initial design and in terms of strength of members as well as relative displacement of floors have exceeded the regulations. Then, in each building, one of the middle frames with a combined system of the flexural frame and convergent bracing is modeled in two dimensions using Open sees software, and the inelastic behavior of the frames in the presence and absence of arm restraints is investigated using increasing nonlinear dynamic analysis of IDA [6]. The results show that structures equipped with arm restraint break at a higher level than the capacity of Sa, and their seismic intensity capacity increases. The relative displacement distribution in the height of the structure shows that in structures without arm restraint, relative displacement accumulation occurred in the inelastic response zone near the middle floors of the structure.

In contrast, relative displacement accumulation occurred in structures equipped with arm restraints. In the lower floors, it leads to the formation of a soft floor mechanism. Therefore, excessive hardening of the structure at a certain level can cause higher modes to dominate the structure's behavior and the possibility of creating a restraint floor at the lower and upper levels. Fragility curves also show that the probability of collapse in structures equipped with arm restraint decreases due to increased structure stiffness. Increasing the height in structures with andwithout arm restraint increases the probability of collapse due to second-order effects.

Research Methods

The present study is applied in terms of purpose and modeling in SAP2000 software. In terms of the data collection method, it is a library method, and then modeling is done. In this research, the required information was collected from the documentary and library method by studying books, articles, and research of other researchers and searching the Internet. Also, using the experiences of technical experts who have conducted useful studies in this field, it was considered the first research stage.

Introducing the software used by Sap2000

The SAP2000 program is a series of SAP programs that is a general program for analyzing and designing structures. The first SAP computer analysis by the Elman Limited method was established about 27 years ago at Berkley University in California. SAP2000 software with high capabilities in modeling different types of structures becomes a powerful general software for analyzing and designing different types of structures. This software is used to analyze various structures such as buildings, industrial structures, tanks, trusses, bridges, and other structures. Its three-dimensional elements are based on a graphically modeled environment in a wide range of engineering analyzes and options. Various project designs are presented in a powerful user interface. SAP2000 is software for all engineers and for any project that can analyze small, simple two-dimensional static concrete formwork. It also provides large and complex 3D templates in dynamic and nonlinear analysis. SAP2000 software responds to all structured analysis and provides the design features needed by engineers.

The most important features of this software are the following:

1. Modeling and analysis of various FRAME, SHELL, ASOLID, and SOLID elements.
2. Modeling and analysis of Kabul elements.
3. Moving loading for bridges.
4. Pressure and heat loading.
5. Static and dynamic nonlinear analysis.
6. Spectral dynamic analysis and linear and nonlinear time history.
7. Analysis of alternating loads.
8. Buckling analysis of structures.
9. Design of steel, concrete, and aluminum structures.

Simple nonlinear analysis with new versions of this software

In the new versions of this software, a nonlinear element, layered coating using a material-oriented model for simple analysis of shear wall structures and similar programs has been added to the program. The Quick-Start section is provided for straightforward modeling of solid concrete sections that demonstrate the capabilities of a nonlinear shear wall.

1. Model design functions have been added to layered coating stresses in new versions.
2. In the to be Designed Section Designer sections, the joints and hinges of the mold to use the number of rebars designed in the program are included.
3. The Section Designer section has been added to display the PMM levels of the fiber model.
4. The properties of the default materials for concreting have been improved to enhance the integrated behavior.
5. Hard tangent surfaces are used to resume the use of joints and fibrous hinges, and the elements of multiline bonding have been changed to improve their integrity.

Dynamic Features

In this program, engineers can use material-based damping for linear and nonlinear analysis of direct integration.

1. Material-based damping is available for PSD analysis and steady-state.
2. At present, the relative damping of hard elements uses their initial hardness instead of the same hardness to improve the consistency of the results and the integrated behavior.
3. This program has added a rigorous calculation in response to response-spectrum model analysis for NRF and general applications.
4. Basic reactions have been improved for the response-spectrum model analysis and the time-history model to protect the connection of spring and ground bonded elements for better access to mass elimination effects [7].

Methods of seismic analysis of structures

There are different methods for seismic analysis of structures. These methods differ in the assumption of linear behavior for structural elements and how seismic force is applied. In linear models, it is assumed that the structural elements have unlimited strength and constant stiffness during the analysis. In contrast, the reduction of structural strength and stiffness during the analysis is considered in nonlinear models. Also, in the static analysis, seismic force is applied to the structure by a static loading pattern. In contrast, earthquake loading is done dynamically in dynamic analysis and based on certain records.

Accordingly, the methods of analysis are:

1. Linear and nonlinear statics:
2. Linear and nonlinear dynamics:

In linear analysis (behavior of linear materials), only the stiffness and strength of the leading members are modeled. In nonlinear analysis, the structural model should include the stiffness and strength of both main primary and non-main members and changes in the strength and stiffness of these members due to reduction. In this study, the dynamic method of nonlinear time history is used, which is described below.

Nonlinear Analysis

Studying the nonlinear behavior of materials and structures is essential because, in severe earthquakes, most structures enter the nonlinear area. Attention to this section follows the application of nonlinear analysis in earthquake engineering and the design of earthquake-resistant buildings. The importance of nonlinear issues in connection with earthquake engineering is the existence of the following parameters in the loading and seismic design of ASCE7:

1. Design force reduction coefficient (behavior coefficient R)
2. C_d displacement increases the coefficient
3. Transmittance coefficient Ω₀

Depending on the type of material at specific stresses, submission and entry into the nonlinear region begin. After that, the yield range of the yielding primary fibers expands to a greater extent than the cross-section. The critical area is the first section to enter the nonlinear region, where a plastic joint is formed. This analysis method is divided into two categories, static and dynamic, whose accuracy depends on many parameters according to the type of analysis. Although elastic analysis and linear evaluation provide a good view of the structure's capacity and the position of the first point of surrender, it can nevertheless predict the mechanism of structural failure and redistribution of forces during successive surrenders. It does not provide reliable results on the amount of plastic deformation and structural damage. Therefore, the analysis and design of new and old structures cannot be justified by linear analysis. On the other hand, for a damaged building whose dynamic properties have changed significantly after the earthquake and for buildings that are to be reinforced with new seismic techniques, it is necessary to study the nonlinear behavior of the structure. The purpose of performing nonlinear analysis with each of the mentioned methods is to determine the maximum plastic change and escape of floors under the earthquake plan so that the seismic performance can be evaluated relative to the structural performance level of the structure.

Nonlinear Dynamic Method (NDP)

The most accurate nonlinear analysis method at present is the dynamic nonlinear time history method, which has not received much attention due to its direct relationship with the selection of seismic records. The use of non-elastic time history analysis is limited and conditional because the dynamic response is very sensitive to modeling and ground motion characteristics. The basis of modeling approaches, analysis hypotheses, and acceptance criteria for nonlinear dynamic analysis is the same as nonlinear static analysis methods. The main difference is that the response results are obtained using time history analysis. In this way, the design forces are not obtained by using the displacement of the target. Instead, they are determined directly by dynamic analysis using the history earth's motion. The responses calculated by nonlinear dynamic analysis are susceptible to the specific properties of ground motion. Therefore, it is recommended that the analysis be performed with more than one ground motion record. In the analysis model, the distribution of energy dissipation devices should be considered both in the plan and in the height of the improved building. If the characteristics of the energy dissipating devices depend on the vibration frequency, operating temperature, deformation or strain, the speed of the incoming loads, and the two-way loads. This dependence must be considered by assuming the upstream and downstream values ​​of the relevant specifications to find the limits of the results in the analysis. Viscous forces in speed-dependent energy dissipation devices must be considered when calculating internal forces and design deformations. Replacing viscosity effects in energy dissipation devices with the overall damping of the structure is not allowed in nonlinear time history analysis. In this method, the deformation and internal forces and, in general, the structure's response are calculated by considering the materials' nonlinear behavior and the structure's non-geometric behavior under a specific accelerometer. In this method, it is assumed that the stiffness and damping matrix can be changed from one step to the next. Still, the intervals of each time step are constant, and the model's response under earthquake acceleration is calculated numerically for each time step.

Effective parameters in nonlinear dynamic analysis results

Member-behavior behavior curve: In the nonlinear dynamic analysis method, the complete hysteresis behavior of each component must be determined. The members' hysteresis behavior depends on the components' type and characteristics, their effort, and even the earthquake.

Acceleration: In the nonlinear dynamic analysis by time history method, the nonlinear response of the structure changes according to the type of acceleration. For this purpose, it is better to use as many accelerometers as possible according to the rules of the regulations.

Nonlinear Dynamic Analysis by Time History Method

The nonlinear time history analysis method is one of the most accurate methods in estimating the response of structures to earthquakes in the range of nonlinear behavior. Achieving accurate results in nonlinear time history analysis requires appropriately selected and scaled accelerometers. In this method, the dynamic analysis of the structure is performed by affecting the ground acceleration as a function of time at the base level and calculating the response of the mathematical model of the structure, which includes its trans-elastic behavior. It is also permissible to use appropriate assumptions about the stiffness and bearing capacity of the foundation according to the soil characteristics and consider flexible support for the structure.

Seismic Fragility Curve

Structural damage forecasting is essential for assessing economic damage in seismic areas. This prediction must have a high degree of validity to reduce the potential for seismic damage. It depends on the seismic performance of the structures in the area where the structure is located. There are two methods to express the extent of damage to structures, which are:

Damage Probability Matrix

The damage probability matrix is ​​in the form of a table. The numbers in the matrix indicate the discrete probability of damage levels for different earthquake intensity levels. The sum of the numbers in each column is one.

Fragility curves

Fragility curves represent the cumulative probability distribution of damage, but the damage matrix indicates the probability of ruptures from the desired level of damage.

As stated, we have a lot of uncertainties in showing how well an earthquake with a certain intensity in the study area brings the desired structure. Uncertainties that play a role in determining instrumental and non-constructive behavior fall into two categories:

1. In the first category, uncertainties are inherent, such as differences in the properties of materials and their resistance to environmental effects.
2. The second category of uncertainties includes sources of error, such as errors in computational methods, modeling, or failure to consider some parameters affecting the behavior of structures or equipment, such as the effect of the frequency content of the input excitation and the input energy of the earthquake. So, the most logical way seems to be to express the structure's performance in probabilistic form. That is, instead of expressing the magnitude of the earthquake that brings the structure to a certain level of performance, express the probability that the structure will reach that level of performance for different seismic intensities [5].

In seismic design based on performance, failure or breakdown occurs when the structure or system in question cannot meet the requirements defined at the desired performance level. If the magnitude of the earthquake is considered the only variable available. In this case, the conditional probability of fragility will be a function of the earthquake's magnitude, called seismic fragility. Therefore, fragility curves express the seismic vulnerability of structural or non-structural components.

F=(D>diIiM)

Where f is a function of fragility and expresses the probability of damage di. D is the amount of damage or equipment estimated in the structure. IM is a schematic of the intensity or magnitude of ground motion.

Analyze

In this study to evaluate the effect of irregular hardness in height on the nonlinear performance of steel structures of flexural frame in the form of calculating the probability of collapse by considering the effect of connection springs for the remote area by modeling and performing dynamic analysis of the possibility of collapse to study four-story structures, the first and third floors and eight floors where the first, third and fifth floors were applied irregularly were modeled in SAP 2000 software, and the results were discussed [7].

Review the Results of the Studied Models

First, the structures were designed to study the behavior of irregular structures, and then time history analyses were performed. Sections from structural design for columns and beams, w type cross-section were used.

The models presented in this research are as follows:

1. Four-story software model without connection spring.
2. Four-story software model with connection spring.
3. Eight-tier software model without connection spring.
4. Eight-story software model with connection spring.

Software Modeling

Balance Connection Spring Mode (4-story structure):The specifications of the sections dedicated to the beams and columns of the structure in the balanced state (1^st floor and irregular) are in the form of 1.

 Figure 1: Sections dedicated to beams and columns in a 4-story structure in balance mode

Figure (2) shows the specifications of the standard connection springs. For the first floor, after the relevant calculations, the amount of sheet thickness for the connection string in this case for the first floor was 0.01 meters.

Figure 2: Specifications of the connection spring for the first floor

Characteristics of normal state connection springs After the relevant calculations, the value of sheet thickness for the connection string, in this case, was considered to be 0.005 m. For the middle openings of the 2nd, 3rd, and 4th floors, the connection spring specifications are assigned in Figure 3.

Figure 3: Chart of connection springs for the second to fourth floors in the middle openings

Specifications of normal state connection springs After the relevant calculations, the value of sheet thickness for the connection spring, in this case, was considered to be 0.004 m. For the side openings of the 2nd, 3rd, and 4th floors, the connection spring specifications are assigned in Figure 4.

Figure 4: Specifications of the connection spring for the second to fourth floors in the side openings

Balance Connection Spring Mode (8-storey structure)

The specifications of the sections dedicated to the beams and columns of the structure in the balanced state (irregular floors 1, 3, and 5) are in the form of (5).

Figure 5: Sections dedicated to beams and columns in an 8-story balance structure.

The source specifications of the normal state connections are assigned in Figure 6. For the first floor, after the relevant calculations, the amount of sheet thickness for the connection spring, in this case, the first floor, was 0.01 m.

Figure 6: Specifications of the connection spring for the first floor.

For the middle openings of the 2nd, 3rd, 4th, 5th, 6th, 7th, and 8th floors, the connection spring specifications are assigned in Figure 7. After the relevant calculations, the thickness of the sheet for the connection spring, in this case, was considered to be 0.005 m.

Figure 7: Specifications of the connection spring for the second to eighth floors in the middle openings.

For the side openings of floors 2, 3, 4, 5, 6, 7, and 8, the connection spring specifications are assigned in Figure (8). After the relevant calculations, the value of the sheet thickness for the connection spring, in this case, was considered to be 0.004 m.

Figure 8: Specifications of the connection spring for the second to eighth floors in the side openings

Mode of Strong Connection Spring (4 and 8-floor structure)

Geometric sections and specifications are done as in the previous section. In the following, the specifications of the connection spring, which is the only difference between this mode and the previous mode, are presented. Finally, the output of the design result is presented. The source specifications of the strong state connections are assigned in Figure (9). After the relevant calculations, the thickness of the sheet for the connection spring, in this case, was considered 0.02 meters.

Figure 9: Specifications assigned to the source of connections in a strong state

After assigning the desired specifications, the design results of these structures can be seen in Figure (10).

Figure 10: Results of sections obtained from the design of a 4-story structure in a balanced and strong state (irregular first floor) 

Table 1: Types of sections resulting from the design of a 4-story structure in a balanced and strong state (irregular first floor)

Figure 11: Results of sections obtained from the design of a 4-story structure in a balanced and strong state (irregular third floor)

Table 2: Types of sections resulting from the design of a 4-story structure in a balanced and strong state (irregular third floor)

Figure 12: Results of sections obtained from the design of an 8-story structure in a balanced and strong state (irregular first floor)

Table 3: Types of sections resulting from the design of an 8-story structure in a balanced and strong state (irregular first floor)

Figure 13: Results of sections resulting from the design of an 8-story structure in a balanced and strong state (irregular third floor)

Table 4: Types of sections obtained from the design of 8-story balanced and strong structures (irregular third floor)

Figure 14: Results of sections resulting from the design of an 8-story structure in a balanced and strong state (irregular fifth floor)

Table 5: Types of sections obtained from the design of 8-story balanced and strong structures (irregular fifth floor)

Table 6: Rota tion time of four-eight-story structures

Increasing Nonlinear Dynamic Analysis of Structures

Another method of nonlinear dynamic analysis is incremental dynamic analysis. Incremental dynamic analysis is a parametric method in which one or more seismic records are each scaled to a certain intensity and applied to the structure. In addition to investigating the seismic behavior of the structure, this method also shows the structure's capacity and can also be used to determine the seismic performance of structures. IDA analysis aims to plot the values ​​related to the size of structural damage at each level against earthquakes. IDA curves are plotted to plot damage size (DM) versus one or more severity measures (IM) based on two or more dimensions independent of IM. In this method, the maximum acceleration value is scaled incrementally from a minimal value, during which the structure's response is elastic and gradually increases until we reach the limit state point after the surrender. In this case, the maximum values ​​of the base shear versus the maximum displacement after each analysis are plotted. The specifications of the acceleration maps applied for the analysis are as follows:

One of the most popular probability estimation methods in the field of structures consists of three random elements. Earth movement intensity, displacement demand, and displacement capacity. It should be noted that this method was created for the SAC2000 project. The intensity of ground motion is selected as the spectral acceleration in the first period of a given structure for particular damping [9]. The combination of the first two elements creates a drift hazard curve.

On the other hand, combining this curve with the third element determines the probability of performance during the year. In addition, PPL as an alternative can be calculated directly using the IM-based method. If we consider the performance rate the same as the collapse capacity, PPL also becomes an annual failure probability. The SAC2000 method provides a solution for determining these values. However, it should be noted that there are some shortcomings in this closed-form solution rooted in simplifying assumptions [9]. For example, consider a constant value for scattering, structure type constraints, etc. However, these can be avoided with the help of direct IDA analysis. One of the most challenging topics in IDA is the many computational activities required for nonlinear reaction history analysis. This becomes even more complicated as the structure gets taller because of extensive computational effort. To reduce these activities, we need to measure the IDA. Different approximation methods have been introduced, which can be summarized in groups of seven.

1. Wamostycosis and Cornell (2004, 2005) introduced SPO2IDA to reduce the time required to reach IDA curves.
2. Baker and Cornell (2005) proposed an epsilon-based filtration solution to select ground-motion recording. This solution takes advantage of Epsilon to reduce the number of ground movement records.
3. Doljak and Fajfar (2005) showed that the N2 method can also be used to approximate the IDA summary curves.
4. Han and Chopra (2006) provide an approximate IDA analysis by increasingly modid analysis of the multi-degree-of-freedom system and dynamic analysis of the one-degree-of-line system of nonlinear freedom, but they may not measure IDA curves. He counted on it for irregular structures.
5. Ghafouri-Ashtiani et al. (2010) aimed to classify the recording of earth movements in groups with different structures. They tried to do this by combining multivariate statistical analysis with principal component analysis. They categorized a wide range of SDOF systems into six different groups and proposed eight registered ground motions for each group to measure the average structural response [4].
6. Mousavi et al. (2011) proposed an eta-based filtration solution, which is a more robust method compared to the epsilon-based filtration solution [10].
7. Azarbakht and Dolesk (2007,2011) presented the IDA, including a record of severe ground movements. On the other hand, they can reduce the computational effort required to achieve IDA summary curves, albeit with a reasonable approximation for MDOF systems. To determine the amplitude of the error and the minimum number of SGMRs, we must measure PPL. A set of SDOF systems are analyzed in this paper. These steps can be described as follows:

Consider a specific scenario of ground movements

Consider a set of SDOF systems with amplitudes from 0.1 to 2 s. It would help if you also considered the ductility, damping, and hardening ratios to cover a wide range of systems and their analysis for the SGMRs defined in the first step. Calculate the best PPL estimate for a complete set of SGMRs for each SDOF system and the approximate PPL for the desired number of SGMRs. To do this, use a list of SGMRs prioritized for the selected scenario and may be obtained by standard seismic hazard analysis or hazard segregation. We get an error if we divide the difference between the two PPL values ​​by the best estimate value.

Table 7: Acceleration characteristics of applied mappings

Figure 15: Spectrum and mean spectrum.

After introducing the above records to the software and scaling them at different intensity levels, finally analyzing all the above records at different levels up to 8g intensity, and then the IDA diagram for general structures, in general, is presented in the figure below. It should be noted that the complete breakdown index based on Hazus tables, as in the table below, is 6%. In this study, it was necessary to apply records up to 8g intensity to reach this criterion.

Investigation of Results of Increasing Nonlinear Dynamic Analysis

The ten different models studied in this research include the four-stage model of balance and strong state, the first and third classes of which are irregular, and the eight-stage model of balance and strong state, of which the first, third, and fifth classes are irregular. Considering that the primary purpose of this research is to investigate the irregular effect of stiffness in height and zone panel on the behavior of structures under increasing load, the diagrams of increasing dynamic analysis are presented and discussed in this section. The following images show the increasing nonlinear dynamic analysis of the following models. This curve shows the structure's interclass drift ratio's maximum response at different seismic application levels. In this structure, Luma and Dozcheh records have reached complete failure at lower earthquake intensity levels, and the structure under the Kobe and Chi Chi records has reached complete failure at higher earthquake levels.

Figure 16: IDA curve for balancing mode of 4-story structure (irregular 1st floor)

In Figure (16), we see which range of acceleration response each of the base records reaches complete failure, and the red line in the figure of the 0.6 drift indicator is a complete failure.

Figure 17: IDA curve for the strong state of 4-story structure (irregular 1st floor)

In Figure (17), we see which range of acceleration response each of the base records reaches complete failure, and the red line in the form of the 0.6 drift indicator is a complete failure.

Figure 18: IDA curve for balancing mode of 4-story structure (irregular 3rd floor).

In Figure (18), we see which range of acceleration response each of the base records reaches complete failure, and the red line in the figure of the 0.6 drift indicator is a complete failure.

Figure 19: IDA curve for the strong state of 4-story structure (irregular 3rd floor).

In Figure (19), we see which range of acceleration response each of the base records reaches complete failure, and the red line in the form of the 0.6 drift indicator is a complete failure.

Figure 20: IDA curve for the balance mode of an 8-story structure (irregular 1st floor)

In Figure (20), we see which range of acceleration response each of the base records reaches complete failure, and the red line in the figure of the 0.6 drift indicator is a complete failure.

Figure 21: IDA curve for the strong state of 8-story structure (irregular 1st floor).

In Figure (21), we see which range of acceleration response each of the base records reaches complete failure, and the red line in the form of the 0.6 drift indicator is a complete failure.

Figure 22: IDA curve for balance mode of 8-story structure (irregular 3rd floor).

In Figure (22), we see which range of acceleration response each of the base records reaches complete failure, and the red line in the form of the 0.6 drift indicator is a complete failure.

Figure 23: IDA curve for the strong state of 8-story structure (irregular 3rd floor)

In Figure (23), we see which range of acceleration response each of the base records reaches complete failure, and the red line in the form of the 0.6 drift indicator is a complete failure.

Figure 24: IDA curve for balanced mode of 8-story structure (irregular 5th floor).

In Figure (24), we see which range of acceleration response each of the base records reaches complete failure, and the red line in the form of the 0.6 drift indicator is a complete failure.

Figure 25: IDA curve for the strong state of 8-story structure (irregular 5th floor)

In Figure (25), we see in which range of acceleration response each of the base records reaches complete failure, and the red line in the figure of the 0.6 drift indicator is a complete failure.

Drawing seismic fragility curves

Porter relations presented in the previous chapter were used to plot the fragility curves. Fragility curves for balance and strength for 4 and 8-story structures are as follows. In Figure (26), the study of seismic fragility of the balanced state of a 4-story structure (irregular 1st floor) showed that the probability of failure at the drift level of 6% is equal to 8%.

Figure 26: Fragility curve for the balanced state of a 4-story structure (irregular 1st floor)

Figure 27: Fragility curve for the balanced state of an 8-story structure (irregular 1st floor)

In Figure (27), the study of seismic fragility of the equilibrium state of an 8-story structure (irregular 1st floor) showed that the probability of failure at the drift level of 6% (complete failure) is equal to 99%.

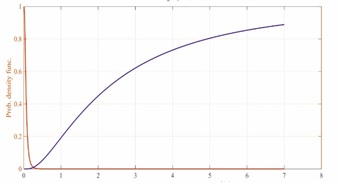
Figure 28: Fragility curve for Foy state of 4-story structure (irregular 1st floor)

In Figure (28), the study of the solid seismic fragility of a 4-story structure (irregular 1st floor) showed that the probability of failure at the drift level of 6% (complete failure) is equal to 83%.

Figure 29: Fragility curve for the strong state of 8-story structure (irregular 1st floor)

In Figure (29), the study of the solid seismic fragility of the 8-story structure (irregular 1st floor) showed that the probability of failure at the drift level of 6% (complete failure) is equal to 96%.

Comparison of Balance and Strong Fragility Curves in two Graphs

Figure 30: Comparison of balanced and strong 4-story structures (irregular floors 1 and 4)

Figure (30) compares the fragility curves of a four-story structure with irregularities on the first and third floors and two balanced and strong zone panel modes. The strong zone panel mode has better behavior.

Figure 31: Comparison of balanced and strong 8-story structures (irregular floors 1, 3, and 5)

Figure 31 compares the fragility curves of an eight-story structure with irregularities in the first, third and fifth floors and two balanced and strong zone panel modes, in which the strong zone panel mode behaves better. A comparison of the two modes of complete and low failure for different modes of irregularity in the floors and the mode of balanced and strong connection spring is demonstrated in Tables 9 and 10.

Table 9: Six percent drift failure (complete failure)

The study of the above results found that the highest seismic fragility and the probability of failure in the balance state occurred for the 8-story structure (irregular 1st floor). The study of the above results found that the highest seismic fragility and the probability of failure is a strong state occurred for the 8-story structure (irregular 5th floor).

Table 10: Half percent drift failure (low failure)

The study of the above results found that the highest seismic fragility and the probability of failure in the balance state occurred for the 8-story structure (irregular 1st floor).

Conclusion

The tendency towards composite structures is expanding due to their proper performance against earthquakes. Further study of the performance of these types of systems can provide a better view. One of the composite systems that are less discussed in Iran is the steel bending frame system with a shear wall. The ten models studied in this research included the four-stage equilibrium and strong state with an irregular first and third classes and the eight-class model of a balanced and robust state with an irregular first, third and fifth classes to draw the fragility curves of Porter relations. The stiffness and strength of the connection spring significantly affect the performance level of the structural components of steel flexural frames. Also, by considering double sheets, the seismic performance of flexural frames is improved, and relative displacement is better controlled. However, increasing its thickness increases the deformation of the beams, and this issue increases the ratio that requires the beams' capacity.

Citation H. Kayhani *, A. Soltani, Assessing the Effect of Irregular Stiffness on Nonlinear Performance of Moment Frame in the form of Calculating the Probability of Collapse at Height for far-field earthquake Considering the Effect of Panel Zone. J. Eng. Indu. Res. 2022; 3(3):203-225.

     https://doi.org/10.22034/JEIRES.2022.4.1    

Copyright © 2022 by SPC (Sami Publishing Company) + is an open access article distributed under the Creative Commons Attribution License(CC BY)  license  (https://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.