Document Type : Original Research Article
Author
Jiangsu University, Research Center of Fluid Machinery Engineering, Azerbaijan
Abstract
Gears are the most significant element of mechanical systems. In this paper, Hertzian contact stress is studied which is one of the main failure causes of gears. As it is known, the rotation motion of meshing gears as a result of torque creates repeated contact stress on the surface of the teeth, and this stress creates fatigue stress in the contact area of the material over a certain period of time. This type of stress is considered as one of the most serious problems of gears, and its optimization is important for increasing the gears’ stability. There are many factors affecting contact stress. In this study, as the most important factors, the contact stress values were measured which modify with the varying values of temperature. Taking into account that contact stress is a theoretical value and cannot be measured practically, the analysis was done by the Finite Element Analysis method using Solidworks simulation software. The contact stress values are measured by means of two gears modeled by applying a high mesh density in contact with each other. The process is repeated in several stages, and the teeth surfaces of each gear in contact are exposed to different temperatures.
Keywords
- Hertzian contact stress
- contact pressure
- thermal effects on contact stress
- optimization of contact stress
- contact stress of hot gears
- contact stress of cold gears
- stress at 25 °C
Main Subjects
Introduction
spur Gear
For this analysis, spur gear was chosen as a gear type. Spur gear is the most widely used type of gear in mechanical processes, and it has many advantages. Some of them are mentioned as follow:
- Simplicity. Spur gear structure is a simple, compact design that makes them easy to design and set, even in restricted spaces.
- Cost-Effectiveness. The simplicity of their design also enables greater manufacturability, making them cheaper to fabricate.
- Constant Speed Drive. These types of gears increase or decrease shaft rotational speed with a high degree of accuracy at a constant velocity.
- Efficiency. Spur gear meshing configurations have power transfer efficiencies between 95% and 99% and can transmit the large amounts of power along multiple gears with the minimum power loss.
- Reliability. Being different from the other motion and power transmission elements, spur gears are unlikely to slide during operation. Along with this, their durability decreases their danger of premature failure.
Contact Stress
In special cases, high stresses can be generated when a load is applied onto a small area of contact. This case typically arises on a small scale when a force is transmitted through two bodies in contact. The excessive contact stresses can cause failures such as cracks and pits in the surface material.
The appropriate determination of contact pressures for complex surfaces is a difficult process. It strongly depends on the geometrical shape of the contacting surfaces.
In industry, a true area of contact is formed according to the immediate deformation of the mating bodies. It depends on the force and the material types from which the parts are made of. The deformation is usually elastic, although some plastic deformation is possible too. These types of stresses were initially investigated by German physicist Heinrich Hertz in 1881.
Contact stress in mating gears is considered as a cylinder contact. The graphical representation of the contact stress between two cylinders is shown in Figure 1 by [1].

Figure 1: graphical representation of the contact stress between two cylinders
Calculation of the max contact stress (pressure) is formulated as below:
 (Equation 1)
(Equation 1)
The half of width b of the rectangular contact area of two parallel cylinders in contact is calculated as:
 (Equation 2)
(Equation 2)
Where,
F: Applied force
E1, E2: Modulus of elasticity for cylinders 1 and 2
ν1, ν2: Poisson’s ratios
L: Length of contact.
Mechanisms of Contact Fatigue
The contact fatigue is a body surface pitting kind of failure. This kind of failure can also be observed in gears, gear couplings, etc. The contact fatigue varies from classic structural fatigue (bending + torsional) in which it results from a contact stress case. This localized pressure case results when curved surfaces have been in contact under a normal force. The contact geometry and the motion of the contacting bodies generate an alternating subsurface shear stress. The subsurface plastic strain is caused by increasing cycles until a crack is formed. The crack then expands till a pit is formed. Once surface pitting has started, the noise level increases. If it is allowed to go on, the fracture of the part and catastrophic failure occurs.
The pressure state generated by contact is concentrated in a small volume of material and creates the intensive plastic strain. The strain accumulates as the same volume is undergone pressure with each cycle until a crack is started. In the true conditions of the contact fatigue, the involved mechanisms can be too complicated. Most models guess a condition of ideal geometric surfaces and some amount of input by heat generation, and in materials’ homogeneity. Hertz stress analysis guesses a circular, ellipse, or line contact surface area between curved surfaces (depending on the geometrical shapes of the contacts) and a parabolic stress distribution with the maximum pressure along the center of the contact.
Examples and Reasons of Heat Generation in Gears
In industrial applications, the excessive temperatures (heat generation) are an undesirable case. As an example, the external gear pump can be shown so that excessive temperature observation in these pumps is an indication of “reduced efficiency” investigated by [3-9] The heat-generating property of the contacts and the exposure of the contacts to the temperature were briefly explained as follow:
Overheating of the gears can be caused by many different reasons, based on the field of application and the mechanical design conditions. As it is known, the fields of gears’ application are incredibly wide, and thus the causes of heat generation are also different. The most common reason is friction between the mating parts. During the friction, a part of the rotational energy transferred from the motor to the gears through the shaft is converted into heat energy, which is the last state of energy. If we look at the reducer sample, we can see how much heat the friction generates. It is precisely for this reason that high temperatures are usually observed in reducers (gearbox). The most common method to reduce this heat is to use lubricants (viscosity adjusted lubricants such as Mobilux-EP2 and Mobilux-EP023 cleared by [2]) is a method that the only selection and lack of lubricants is another reason for the heating of gears.
The external effects can be another reason why gears become hot or cold. An external and internal gear pump can be shown as a sample. In these kinds of pumps, the temperature of the liquid transported by means of the gears is further set on the gears, so the gears can be heated and cooled to the desired temperature in these types of applications due to the application features.
Finite Element Analysis
Model Information:
Two gears with high mesh density have been modeled in Solidworks software. Gears are of the same dimensions:
Number of teeth: 20
Module: 50
Pressure angle: 20 degrees
Face width: 100 mm
Nominal shaft diameter: 200 mm
Details of the analysis:
Material: Gray Cast Iron
Number of nodes: 90055 nodes
Total elements: 58955
Applied torque: 100 N.m
In Table 1 are the characteristics of gray cast iron taken from the Solidworks library:
Table 1: gray cast iron parameters (Solidworks)

Boundary Condition
In this study, one of the gears is at a fixed position, and the fixture is chosen to be the internal cylindrical face of the shaft as a fixed geometry. However, the second gear is given torque of 100 N.m and the internal cylindrical face is chosen as fixed hinge. The rotating gear’s tooth compresses the first gear’s tooth face, which is at a fixed position, and so compressive stresses are generated that cause the contact pressure in Figure 2.

Figure 2: gears in meshing generating contact stress
Results
In Figure 3 and 4, the contacting gear tooth faces have been exposed to 50 C and the resultant max contact stress has been calculated through FEA.

Figure 3: mesh view

Figure 4: contour view
According to the series of simulations done by the author, the maximum contact stresses at variations of temperature are shown in Table 2:
Table 2: measured parameters list
|
5 °C |
6,49739 MPa |
|
10 °C |
4,80354 MPa |
|
15 °C |
3,10849 MPa |
|
25 °C |
0,07450 MPa |
|
35 °C |
1,66562 MPa |
|
50 °C |
3,98838 MPa |
|
70 °C |
7,08520 MPa |
|
90 °C |
10,17838 MPa |

Figure 5: EES added data
The collected data (Figure 5) is added to EES (Engineering Equation Solver) software and plotted in Figure 6. It is observed that the dependence between the maximum contact stress and temperature is totally linear for each region.
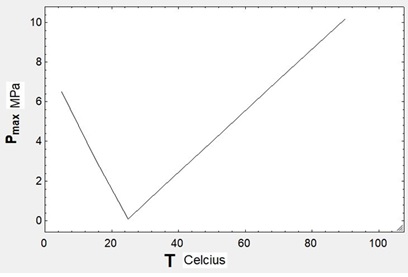
Figure 6: Hertzian contact stress vs temperature graph
Subsequently, both lines from colder to middle point and middle to hotter point are fitted by a “curve fit” function that enables us to extract the most appropriate formula between two parameters. The graph in Figure 7 indicates that “fitted” lines and original lines are completely on the same alignment, so there are exact proportional and inversely proportional relations between the max contact stress and surface temperature.

Figure 7: curve fitted graph and obtained formulas
Conclusion
In conclusion, in this study, the variations of contact stress, which is the most important failure criterion for gears, at different temperatures were calculated. The obtained values as a result of Finite Element Analysis indicate that the contact stress reaches its maximum at very cold and hot temperatures, and both these temperature states are dangerous for gears. Until 25-26 C contact stress is inversely proportional to temperature and dependency is completely linear. On the other hand, the contact stress is proportional to temperature after 25-26 C and dependence is completely linear. The most ideal temperature is 25-26 C, which is approximately room temperature, because at this point the contact stress is lower than colder temperatures, the contact stress decreases, and the design condition becomes ideal and reaches its optimal range at 25-26 C. However, as the temperature rises to points hotter than 25 C, the contact stress begins to increase again due to the additional "thermal stress" created by the temperature. Taking all these into consideration, we can make the inference that both very hot and very cold temperature conditions are dangerous for the stress behavior of gears, and the medium temperature ranges are the most suitable option for the ideal design conditions.
Citation A. Ibrahimov*, Effects of Temperature on Spur Gear Hertzian Contact Stress and Plotting of Graph for Gray Cast Iron by Finite Element Method. J. Eng. Indu. Res. 2022; 3(4):257-264.
https://doi.org/10.22034/jeires.2022.4.6
Copyright © 2022 by SPC (Sami Publishing Company) + is an open access article distributed under the Creative Commons Attribution License(CC BY) license (https://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
- Castro Guzmán J.M., Análisis de esfuerzos hertzianos de elementos de maquinas en MATLAB (Bachelor's thesis, Universidad EAFIT), 2005 [Google Scholar], [Publisher]
- Ghewade D.V., Nagarale S.S., Pandav A.N., Heat Generation Analysis and its Reduction in Meshing Gears, International Journal for Ignited Minds (IJIMIINDS), 2016, 3, 2349-2082 [Google Scholar], [Publisher]
- Dalla Lana E., De Negri V.J., A new evaluation method for hydraulic gear pump efficiency through temperature measurements, SAE Tech. Pap, 2006, 01, 3503 [Google Scholar], [Publisher]
- Popov V.L., The book “Contact Mechanics and Friction” Physical Principles and Applications, Springer Publishing, Berlin, 2009 [Google Scholar], [Publisher]
- Khurmi R.S., Gupta J.K., A textbook of machine design. S. Chand publishing, 2005 [Google Scholar], [Publisher]
- Johnson A., Investigation of Network Models Finite difference Method, Eurasian Journal of Chemical, Medicinal and Petroleum Research, 2023, 2, 1-9 [Google Scholar]
- Lo Han K., Investigation of Heavy Polyethylene Catalytic Pyrolysis, Eurasian Journal of Chemical, Medicinal and Petroleum Research, 2022, 1, 64-70 [Google Scholar]
- Rebout F., Effect of Polymers on Transient Reynolds Number Change in Pipe Flow and Reduction of their Coefficient of Friction, Eurasian Journal of Chemical, Medicinal and Petroleum Research, 2022, 1, 20-32 [Google Scholar]
- [9] Alizamin Ibrahimov.” Double Tooth Contact Effects on Spur and Helical Gears”. Journal of Engineering in Industrial Research, 2022; 3(4):249-256 [Crossref], [Google Scholar], [Publisher]

