Introductio

 Float zone furnaces are designed such that the heat produced is restricted to a very narrow area or annulus. The narrow heated zone is useful for material refining; especially semiconductor crystal growth in industrial and research facilities. There are several types of these heat production devices that are useful in this type of furnace. They include high frequency or induction heaters, [1-3] electrical resistance heaters [4-6], electron beam and plasma heaters, [7] lasers, [8-11], and lastly thermal radiation focusing [12-35]. The resistance heaters have large physical size limitations as well as large heat areas, induction heaters require electrically conductive samples, electron beam, and plasma cathode material may contaminate samples while laser heating is quite complex and has low efficiency.

The thermal radiation furnace also known as image or optical furnace focuses thermal radiation onto sample material using curved mirrors such as concave, elliptical, ellipsoidal, and some high temperature lenses. The furnace is characterized by high energy efficiencies, high processing temperatures, ability to process very small quantity of materials under controlled conditions [36], and can be fitted with cameras for visual control of crystal growth. Heat is transferred to the sample through convergence of beams of radiant energy at the second focus, where the sample is located. These furnaces are quite expensive and make use of proprietary technologies and are rarely found in research laboratories.

Commercial optical furnaces are produced without graduated temperature settings; instead with input lamp power settings and in order to be used, their temperature profiles have to be determined through pre-trial runs on samples embedded with thermocouples. This is however not practicable for actual float zone crystal growth since the thermocouple material would contaminate the material crystal being produced. Koopayeh et al. (2009) [37], in his pre-trial of a newly acquired float zone furnace, observed that the shape of the lamp power versus sample temperature relationship was quite complicated. He also observed that sample temperature does not only depend on the lamp power, but also on the sample’s physical properties. However, no attempt was made to simulate the relationship.

Behr et al. (2010) [38] is reported to have used optical pyrometry to determine the temperature profile through the use of shutters that intermittently shut off the lamp source while recording only the radiation from the sample under study.

Jonathan et al. (2020) [39], on the other hand, developed an optical furnace with provision for X-ray beam sampling where the data generated was thereafter, related to the sample temperature profile after processing with relevant computer software. The procedures used were quite complicated especially with software in data refinement and processing.

Yildrim et al. (2020) [40] built an optical furnace for dark field X-ray microscopy in which the temperature was calibrated using the lattice parameter and thermal expansion of α-iron grain as well as k-type thermocouple, respectively. A polynomial was fitted to the temperature versus power plot from the k-type thermocouple data; however, only four data points were used and no goodness of fit was mentioned. The data from the lattice and thermal expansion characterisation was used to generate temperature versus power plot with a good fit having twenty-three data points; however, the fit function was not specified.

Yan et al. (2016) [41] in their study of temperature gradients around the molten zone of TiO₂ feed rod, using a four mirror optical furnace, attempted to establish the relationship between lamp power and temperature gradient as well as filament geometry and temperature gradient with the aid of finite element modelling. Their result was compared with the experimentally measured temperature gradients although temperature measurement device and technique were not stated.

Guanglong et al. (2021) [42] used many physical parameters (such as density, sample dimensions, heat capacity, thermal conductivity, emmisivity, for sample and sample holder, respectively, as well as lamp parameters and algorithm parameters) optimization with the aid of machine learning, to simulate steady state temperature variations in Al₂O₃ in sample and power absorbed by sample. The result was in agreement with experiment as shown in the plot of temperature versus axial distance; however, this was done for five lamp power settings. A polynomial fit was done for the plot of absorbed power (obtained from the simulation) versus lamp power; however, no goodness of fit was reported. Besides, the model was reused by Wang et al. (2021) [43] where it was modified to include, sample environment data such as various ambient atmosphere (vacuum, air, argon, and helium), fused silica glass tube capsule effect and sample holder effect on the sample temperature rise and cooling. The results were sample temperature variations with axial distance, but no temperature versus lamp power was reported.

Scott and Jeffrey (2022) [44] studied crystal growth behaviour in a single lamp double mirror, HKZ (Hochdruck-Kristallzüchtungsanlage), optical floating zone furnace, under high pressure, using thermal capillary modelling. In their findings relating to temperature distributions, they were able to relate the temperature distribution, in the molten zone, to radial distance. However, no study was reported relating temperature distributions to applied lamp power. It is against this background that we present our simpler and cheaper design; using aluminium alloy ellipsoidal flood light reflector based thermal radiation furnace for the experimental study of the relationship between sample temperature and applied lamp power. The effect of sample physical properties would be ignored at this stage and as such the determined relationship would only be applicable to samples with similar physical property such as colour. Once this is established, further research would be aimed at determining the effect of sample properties on the temperature growth curve. This is yet to be reported in available published literatures.

The working principle of the thermal radiation float zone furnace is the focusing of infrared energy using ellipsoidal mirror imaging technique. The image of an object placed at the primary focus is replicated at the secondary focus. In this case, an image of the heat source (halogen filament) at the primary focus is replicated at the secondary focus; thereby acting as a remote heater on any object located in that area. Figure 1 displays several optical arrangements used in different thermal radiation furnaces for achieving proper temperature distribution at the secondary focus where the object to be heated is placed. 

Figure 1: Different optical configurations of the image furnace (a) two mirror paraboloidal system, (b) single ellipsoidal system, (c) multi-ellipsoidal system, and (d) condenser-relay lenses or refractive system

Theoretical Background

The design of the furnace is primarily based on rectilinear propagation of light at curved surfaces such as an ellipsoidal mirror or reflector and heat and thermal radiation transfer between the two foci within the mirror enclosure.

The Ellipsoidal Reflector

The ellipsoidal reflector is a three dimensional ellipse, as shown in Figure 2, and mathematically described by Equation (1) in the Cartesian coordinate system. The length Oa which is half ‘aa’ is the semi-major axis while the length Ob which is half ‘bb’ is a semi-minor axis while length Oc which is half ‘cc’ is the second semi-minor axis.

Two points f₁ and f₂, known as the foci, are important reference points in the definition of an ellipse. The distance between the centre of the ellipse and focus f, is usually labelled c for a one dimensional elliptic curve; however, for a three dimensional elliptic curve the third axis is labelled, c, hence we have adopted the letter g. The relationship between focus and the other axes is given by Equation (2).

Figure 2: An ellipsoid with some defining parameters

               (1)

              (2)

The eccentricity is a measure of how close the ellipse, is to a circle or a sphere in the case of an ellipsoid is defined by Equation (3).

                  (3)

The distance a-f, i.e. the distance of the focus from the ellipsoid apex axis, determines the heat source location in order for the image of the heat source to be focused at the secondary or conjugate focus where the sample to be heated would be located.

The Surface Area of an Ellipsoid

The surface area of an ellipsoid is important for thermal radiation heat transfer considerations. Surface area is determined using the ellipsoid dimensions as given in Equations (4) and (5) [45,46].

      (4)

            (5)

Heat Transfer in the Image Furnace

The image furnace functions basically on the principles of heat transfer by thermal radiation focusing aided primarily by the reflective internal walls of the ellipsoidal enclosure and its unique elliptic focusing property. According to the Stefan-Boltzmann law, the rate R at which heat is emitted from a unit area of a heated body at absolute temperature T is given by Equation (6).

       (6)

Where, e is emissivity of the body and s is Stefan-Boltzmann constant 5.672 x 10^-8 (W/m²K⁴). For a heated body at absolute temperature T_s, enclosed by another body at temperature T_m, the net heat radiated, is given by Equation (7).

       (7)

For any given surface area A, the net thermal radiation is given by Equation (8).

          (8)

For an image furnace setup consisting of a filament lamp of input power P_l, sample of surface area A_s with the supporting sample stand having conductivity B, the  radiation received by the sample is equal to total losses by the sample at steady state temperature [10].

        (9)

          (10)

Where, A_o is the area of the open top of the ellipsoid, A_s is the lateral area of the of the sample (adjacent to the mirror surface), P_cond is the power loss by conduction through the sample and support, and P_ls is the radiation power received by the sample from the lamp and is given by Equation (10) assuming negligible loss at the lamp base.

Some conductive losses occur at the lamp base thus reducing the lamp power. We account for this by estimation, thus effective lamp power P_eff will be given by Equation (11) and P_ls can be rewritten as Equation (12).

  (11)    

  (12)

Where, r, is the reflectivity of the ellipsoidal mirror. Radiation lost by lateral surface A, of sample to the blackbody radiation inside the ellipsoid is given by Equation (13).

       (13)

Radiation lost by thermal conductivity of sample holder is given by Equation (14).

         (14)

Where, B is the thermal conductivity of the sample holder.

Radiation lost by top surface of sample to the outside environment is given by Equation (15).
      (15)

The ellipsoidal mirror material itself contributes to losses as a result of the imperfect reflectivity and this is given by Equation (16).

       (16)

Where,

     (17)

is the fraction of input power loss to mirror by absorptivity during reflection while

                                                               (18)

Equation (18) is the eventual radiation loss by the blackbody radiation in the enclosure to the environment (ambience).

Again, in the steady state, the radiation lost by the surface area of the sample adjacent the mirror’s surface at the secondary focus region, is equal to the radiation absorbed by the mirror [19].

Therefore,

  (19)

        (20)

Solving for T_in⁴ in Equation (20) and substituting into Equation (9), we get Equation (21)

                                                                                                                                                                                                                                  (21)

But,

         (22)

Where, B is the thermal conductivity of the quartz sample holder. Substituting Equation (22) into (21) and solving for Ts4 we get:

  (23)

       (24)

This equation can be re-written as:

       (25)

Where,

 (26)

                                                                                                                                                                                                                                   (27)

By evaluating the constants C and D and estimating B, the furnace temperature Ts , can be determined.

Materials and methods

Ellipsoidal Furnace Design and Implementation

The design was based on the best available commercial ellipsoidal floodlighting reflectors in the local market. Two (2) reflector-grade aluminium, floodlighting reflectors of semi major axis a = 31.0 cm, semi minor axes, b = c = 25.5 cm, and eccentricity e = 0.587 with the best surface profile and reflectivity were acquired. According to Elmer [47], reflectivity r of reflector grade aluminium lies between 0.79-0.83. The two halves of the ellipsoidal reflectors in Figure 4 were joined at their base to form the complete ellipsoid. The focal length of the ellipsoid was determined to be 13.00 cm; however, the experimentally determined focus was 4.5 cm. A halogen lamp (model: FTM 64788 CP/72 Philips 2000 W, 230 V) having a clear glass envelope was obtained and firmly secured into its holder at the lower focus of the ellipsoid to serve as a heat source as shown in Figure 3. The outer surface of the ellipsoid was cooled using eight (8 mm) copper tubing carrying pressurized running water with the aid of a 0.5 HP water pump. Further cooling was achieved by connecting the water line to a small radiator.

Figure  3:  Ellipsoidal reflectors, showing (a) dull back surface, (b) shiny interior surface and two rectangular filament lamps, 2000W 230V, (c) G38 base-type, and (d) GY16 base-type

Figure 4: The ellipsoidal furnace schematic

The opening at the top of furnace was covered with some number of flat asbestos sheets, wrapped with aluminium foil, and having a 2.40 cm diameter hole in the centre to hold a quartz tube of length 30 cm that serves as a sample holder. The completed setup is depicted in Figure 5.

Figure 5: The assembled furnace and the cooling accessories

Ellipsoidal Furnace testing and Temperature Characterization

The completed image furnace is powered by a halogen lamp, rated 230 V, 2000 W. The current-voltage characteristic of the lamp was determined by measuring current as a function of the supply voltage. The conjugate focus was then validated from temperature-distance measurements along the azimuth. The selected lamp voltages were used to establish steady state temperature-voltage relationship at the conjugate focus.

The temperature profile at distances, away from the conjugate focus along the axis of rotation of the ellipsoid  and at radial distances from the conjugate focus were determined from measurements using a K-type thermocouple connected to a temperature data logger (TES 1315  thermometer).

Results and Discussion

Current Voltage (I-V) Characteristics of the Halogen Lamp

The current voltage (I-V) characteristics determination was done using the measurements obtained from the circuit in Figure 6, where the selected mains voltages, ranging from 0 to 180 V were applied to the lamp using a variable transformer. Voltage drop across the lamp filament as well as current through the lamp were measured using digital multimeters. The result of the measurement is shown as the plot in Figure 7.

Figure 6: The circuit for the measurement of I-V characteristics of the halogen lamp tungsten filament

Figure 7: Current -voltage characteristics of the halogen lamp used in the ellipsoidal mirror furnace with a non-linear fit model

Figure 7 shows a model fit of experimental current and voltage data distribution of the halogen lamp used as the heat source of the mirror furnace. The current-voltage relation data was fitted with a power law model using chi-square analysis integrated into the nonlinear curve fit option of Originlab software version 2019b. The fit has very high R-square and adjusted R- square values of 99.87%, respectively, and relatively low reduced chi squared value of 6.58 compared to the critical value of 49.8 at 5% significance level and thirty-five (35) degrees of freedom. The null hypothesis that the experiment data distribution is not different from the model fit is hereby accepted. This current-voltage relationship can be stated as current in the filament is proportional to the voltage raised to a fractional power and this is represented by Equation (28).

[]    (28)

Similar relationship has been reported by other researchers [48].

Temperature-Time Variation at Select Axial Distances from the Conjugate Focus of the Ellipsoidal Mirror

The temperature variations with time at selected axial distances from the conjugate focus were measured and the result is demonstrated as the plot in Figure 8.

This was necessary to validate the theoretically determined focus which is the point of maximum temperature where the sample will be placed.

Figure 8: Variation of axial temperature ( C) with time (min) at selected distances (cm) from the opening of the ellipsoidal mirror to the conjugate focus and beyond

The theoretically determined focus is 13.00 ± 0.10 cm whereas the experimental focus is 7.5 ± 0.10 cm. This large discrepancy could not be explained by the usual deviations reported by previous researchers but might be attributed to the flood lighting optimizations of the reflector.

Ellipsoidal Mirror Conjugate Focus Temperature Variation with Lamp Supply Voltage and Power

The maximum steady state temperature at the conjugate focus where the sample is placed is dependent on the applied lamp voltage.

A relationship has been determined from the measurement, of the steady-state temperature of the small bead and of a K-type thermocouple placed at the focus and corresponding input voltage supplied by a variable transformer, as illustrated in Figures 9 and 10.

Figure 9: Temperature variations (a) in ( C) and (b) in (K) at the conjugate focus of the ellipsoidal mirror furnace

Figure 10: Temperature variations (a) in ( C)  and (b) in (K) at the conjugate focus of the ellipsoidal mirror furnace for selected lamp power supply (W)

Sample temperature variation is a very crucial characteristic of the ellipsoidal mirror furnace. Once in operation, it is difficult to measure the temperature of the sample material at the point of heat application without affecting or contaminating the sample since, one of the advantage of the furnace is that the sample would be free from contamination; even from the temperature measuring device. Two-curve fits of the temperature T ( C) and (K) versus lamp voltage V using a nonlinear model known as inverse-exponential in Originlab software version 2019b were carried out. The furnace temperature T ( C) and T (K), were related to the applied lamp voltage V, as shown in Figures 9 and 10 and resulting constant coefficients have been used to express the relationships in Equations (29) to (31). Both fits have good R- square and adjusted R- square values as well as low “reduced chi squared” values of 30.96 and 36.26 that are statistically significant since they are less than the critical value of 49.8 and corresponding P-values of 0.66 and 0.41 which are greater than the 0.05 value of the null hypothesis. Thus, the null hypothesis that the experimental data distribution is not different from the model fit is accepted. The comparison of both model results with the experimental data is as shown in Figure 11.

    (29)

(30)

(31)

Similar relationship was also obtained for temperature versus lamp power, as shown in Equations (32) and (33).

    (32)

     (33)

Figure 11: Comparing temperature (K) variation at the conjugate focus of the ellipsoidal mirror furnace at selected lamp supply voltages (V) for experimental data with those  determined by two inverse exponential model fits using Chi-square analysis integrated in the Originlab software, i.e. relating

temperature ( C) and (K) to Lamp supply voltage

Analysis of Constants (a, b, and c) in T-V Relationship

To determine the significance of the constants a, b, and c in the temperature-voltage relationship, the equation was “linearized” by taking the natural logarithm and comparing the resulting equation with that of a straight line.

Recall Equation (29):

In this equation, b and c will have the units of the lamp supply voltage (V).

  (34)

Let

(35)

And

  (36)

Then, we can rewrite Equation (34) as follow:

  (37)

      (38)

    (39)

The constant ‘b’ is the slope of the straight line and it determines comparative growth-rate of the temperature-voltage curve in Equation (29).

Therefore, the slope

    (40)

Where, T2 > T2; V2 > V1 and 1/V2 < 1/V1

   (41)

     (42)

The constant ‘c’ which is referred to as an offset voltage, determines the magnitude of the initial or ambient furnace temperature.

Then, by plotting the natural log of the experimental temperature data against the inverse of the applied lamp voltage and an offset value c = 26.79 V, a straight line is generated as shown in Figure 12.

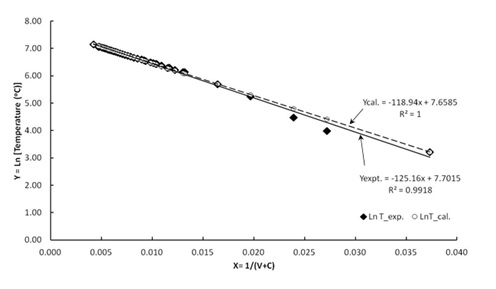
Figure 12: Variation of Ln (Temperature (^oC)) with  1/(V + c)

Note: This is to enable the ‘linearization’ of the relation T = exp (a+b/(V + c)), i.e. Ln( T ) = a + b/(V + c) for experimental data (T_exp.) and for fitted data (T_cal), where T is the furnace temperature (^oC) and V is the applied voltage (V).

From the plots in Figure 12, two straight line equations with their R squared values have been generated using Microsoft Excel charting programme.

   (43)

  (44)

Where, Equation (43) is for the fitted temperature data and Equation (44) is for the experimentally acquired temperature data. The intercept, on the Y– axis (LnT)  is the constant ’a’ in Equation (37) and determines the theoretical maximum furnace temperature achievable at a theoretical maximum applied voltage for which Equation (45) holds.

    (45)

i.e. for

The constant ‘-125.16’ is the slope of the straight line with the intercept used for the computation of T_max and this is the constant ‘b’. It determines comparative growth-rate of the temperature-voltage curve in Equation (29).

Therefore the slope is as given in Equation (42).

The constant ‘c’ which is likened to an offset voltage, corresponds with the magnitude of the initial or ambient furnace temperature.

The Conjugate Focus Axial Temperature Profile

The variation of the temperature of the region, along the conjugate focus, parallel to the axis of rotation of the ellipsoidal mirror is an important characteristic of the radiation furnace for use in zone melting applications. The steady state temperature distribution with distance along the axis of rotation, was measured at 84 V lamp supply by placing the bead of a K–type thermocouple at selected distances before and after the conjugate focus position. Figure 13 shows the temperature distribution as a function of distance (mm) from the conjugate focus parallel to the axis of ellipsoid rotation.

Figure 13: The temperature distribution (a) in (^oC) and (b) in (K) along the conjugate focus parallel to the axis of rotation of the ellipsoid with a lamp supply voltage of 84 V

Similar trends have been observed by previous researchers although most have measured flux distributions or irradiance [49-51] instead of temperature [12-13,21,24,52].

The Conjugate Focus Radial Temperature Profile

The temperature variation around the conjugate focus was also measured at selected distances perpendicular to the axis of rotation of the ellipsoid. These variations determine the maximum size of sample that can be heated effectively. The thermocouple was attached to a rigid wire that suspends the bead at selected distances from the conjugate focus. The steady state or quasi steady state temperature was measured at regular intervals of two (2) mm. After each measurement, the furnace is cooled to near room temperature and the process repeated for other radial distances. Figure 14 shows the obtained temperature distribution.

Figure 14: Temperature distribution (K) around along the radial direction (mm) of the conjugate focus of the radiation furnace powered by 84V a.c supply

The curve is also nearly a Gaussian fit and similar to what has been observed by previous researchers [49-50,53,54-57].

Analysis of the Efficiency of the Image Furnace

The theoretical efficiency h is the ratio of the thermal radiation reaching the sample to the electrical power supplied to the lamp. The thermal radiation reaching the sample was deduced from Equation (12), while the electrical power supplied is 2000 W at maximum operating voltage.

 (46)

  (47)

  Experimentally determined efficiency of the completed ellipsoidal furnace is the ratio of the input power (i.e. power supplied to the lamp) to the output power at the conjugate focus where the sample is located. Electrical power (IV) in watts is supplied to the lamp as shown in Equation (48).

                                                                                                               (48)

The sample receives thermal radiation power over its surface area as shown in Equation (8).

The emissivity e of the fired clay rod is 0.91 [58]. For a fired clay rod of length, L = 24 mm = 0.024 m, diameter D = 12 mm = 0.012 m, and at a steady state temperature of 1,183 ^oC (1,456 K) when lamp power was 1592.46 watts.

 (49)

This is for the clay sample and does not represent the actual efficiency since the sample did not maximally absorb.

The efficiency of the ellipsoidal float zone furnace was determined via the measurements of the power supplied to the lamp and the determination of the thermal radiation from a known sample surface area at a steady state temperature. The efficiency was found to be 16.44% for a fired clay sample of emissivity of 0.91 while the theoretical efficiency was determined to be 68.6%. This efficiency is rather low compared to what other researchers have reported but should be understood based on the optics of the system (ellipsoidal flood light reflectors) which can be mentioned to be optimized for aerial lighting and good heat dissipation.

Conclusion

The axial and radial temperature variations of the thermal radiation furnace with distance were found to approximate a Gaussian distribution, respectively. For a given sample and furnace specifications, the temperature is found to be inverse-exponentially related to the applied lamp voltage. There remains the problem of relating the inherent constants in the regressed model, to specific sample physical properties such as dimension, shape, colour, or absorptivity. Hence, this would be a relevant area for future research. The significance of this work is that it would make the recalibration of lamp voltage or power of an optical furnace in terms sample temperature easy when the constants in the temperature equation are known. In other words, this can help with profiling any other thermal radiation furnace by substituting relevant sample physical constants and furnace optical constants into the regressed model to determine appropriate temperature that can be achieved with any given lamp power. 

Citation E.B. Otokunefor*,  S.O. Azi. A Float Zone Furnace Using Ellipsoidal Flood Light Reflectors. J. Eng. Indu. Res. 2023, 4 (2):110-129.

     https://doi.org/10.48309/JEIRES.2023.2.5  

Copyright © 2023 by SPC (Sami Publishing Company) + is an open access article distributed under the Creative Commons Attribution License(CC BY)  license  (https://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.